1 - Nadkvadrat

ZadatakRešenje

Vremensko ograničenje	Memorijsko ograničenje
100ms	32MB

Dobro je poznato (još od 1888. godine i Ničeovog dela Sumrak idola) da ono što nas ne ubije - to nas ojača. Tako je i sa tačkama, kvadratima, takmičarima, pa i samom komisijom... Ako već ne može da kao ranije organizuje tri kruga kvalifikacija, komisija može zadati tri tajna broja (videti prošli krug) i tri javne tačke u ravni (gledate ih upravo). Ako već tačno tri godine, još od doba poslednje pandemije (i drugog kruga kvalifikacija školske 2020/2021. godine), niko i dalje ne pita kako je kvadrat?, a on preživi, postaće nadkvadrat (nem. Überquadrat) i obuhvatiće sve tri javno zadate tačke!

Naime komisija je zadala tačno tri tačke u Dekartovom pravouglom koordinatnom sistemu u ravni definisane celobrojnim koordinatama \((x_1, y_1)\), \((x_2, y_2)\) i \((x_3, y_3)\). Vaš zadatak je da pronađete površinu najmanjeg kvadrata sa stranicama paralelnim koordinatnim osama koji ih sadrži, odnosno obuhvata sve tri zadate tačke!

Opis ulaza

U prva i jedina tri reda standardnog ulaza nalaze se celobrojne koordinate tačaka i to: u prvom redu \((x_1, y_1)\), u drugom redu \((x_2, y_2)\) i u trećem redu \((x_3, y_3)\). U svakom redu koordinate \(x\) i \(y\) su razdvojene razmakom.

Opis izlaza

U prvom i jedinom redu standardnog izlaza, ispisati površinu najmanjeg kvadrata sa stranicama paralelnim koordinatnim osama, odnosno pravama \(x=0\) i \(y=0\), koji obuhvata tri zadate tačke.

Primer 1

Ulaz

1 2
3 3
2 1

Izlaz

4

Objašnjenje

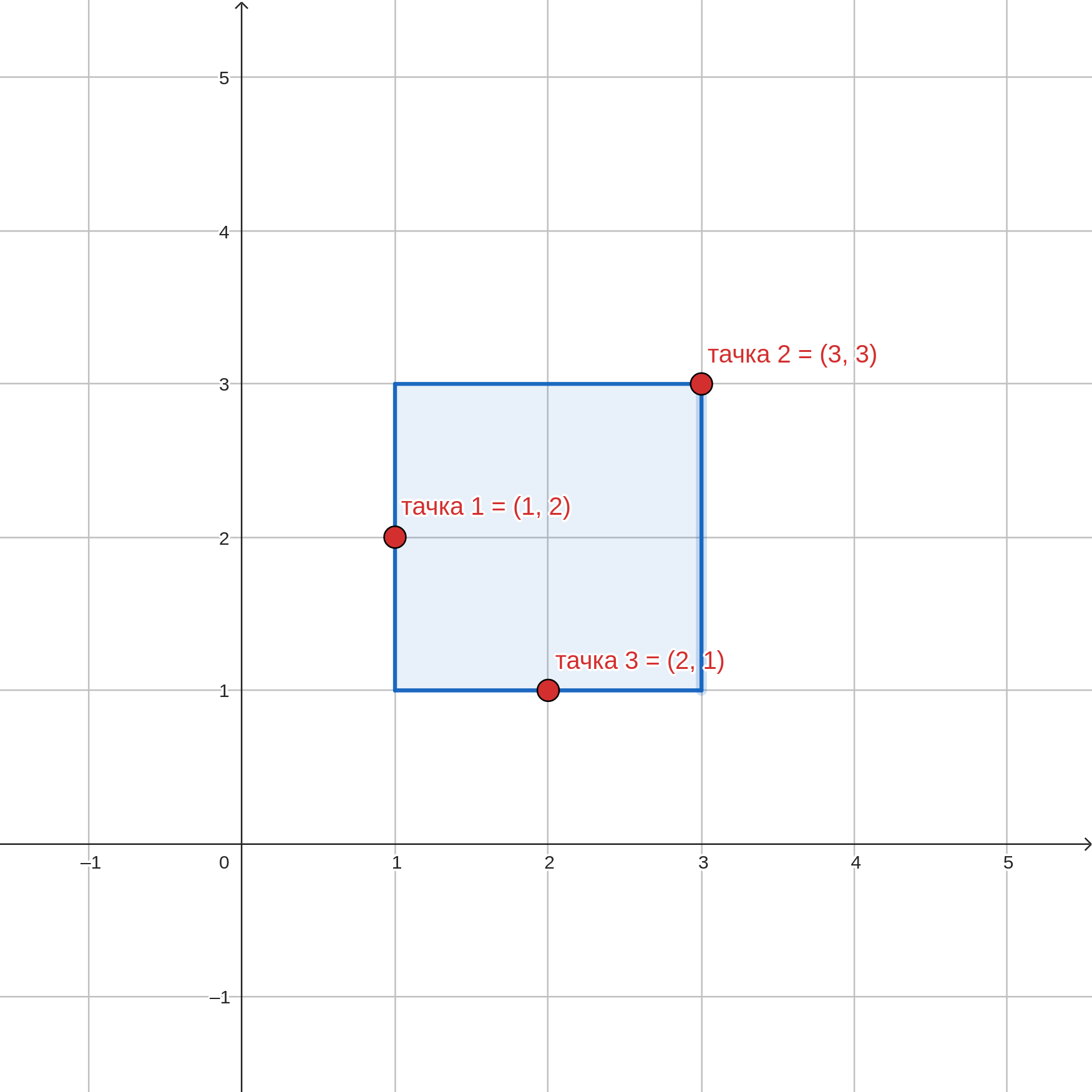
Tri tačke koje su zadate mogu se obuhvatiti kvadratom čije će donje levo teme biti u koordinati \((1, 1)\), a gornje desno teme u koordinati \((3, 3)\) te je njegova površina \(2^2=4\).

Primer 2

Ulaz

1 1
-2 -1
3 -2

Izlaz

25

Objašnjenje

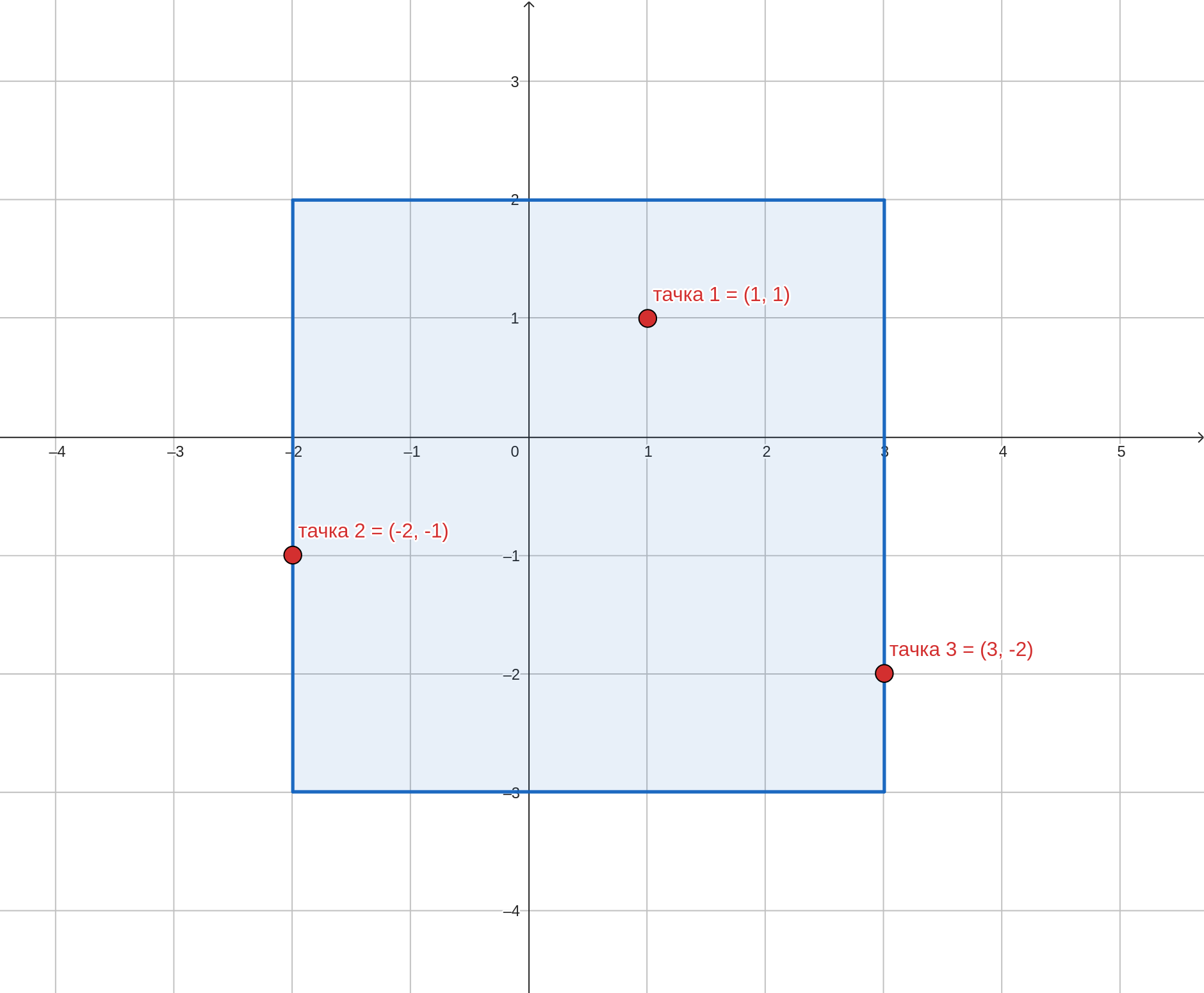
Tri tačke koje su zadate mogu se obuhvatiti kvadratom čije će donje levo teme biti u koordinati \((-2, -3)\), a gornje desno teme u koordinati \((3, 2)\) te je njegova površina \(5^2=25\).

Primer 3

Ulaz

1 2
3 4
5 6

Izlaz

16

Objašnjenje

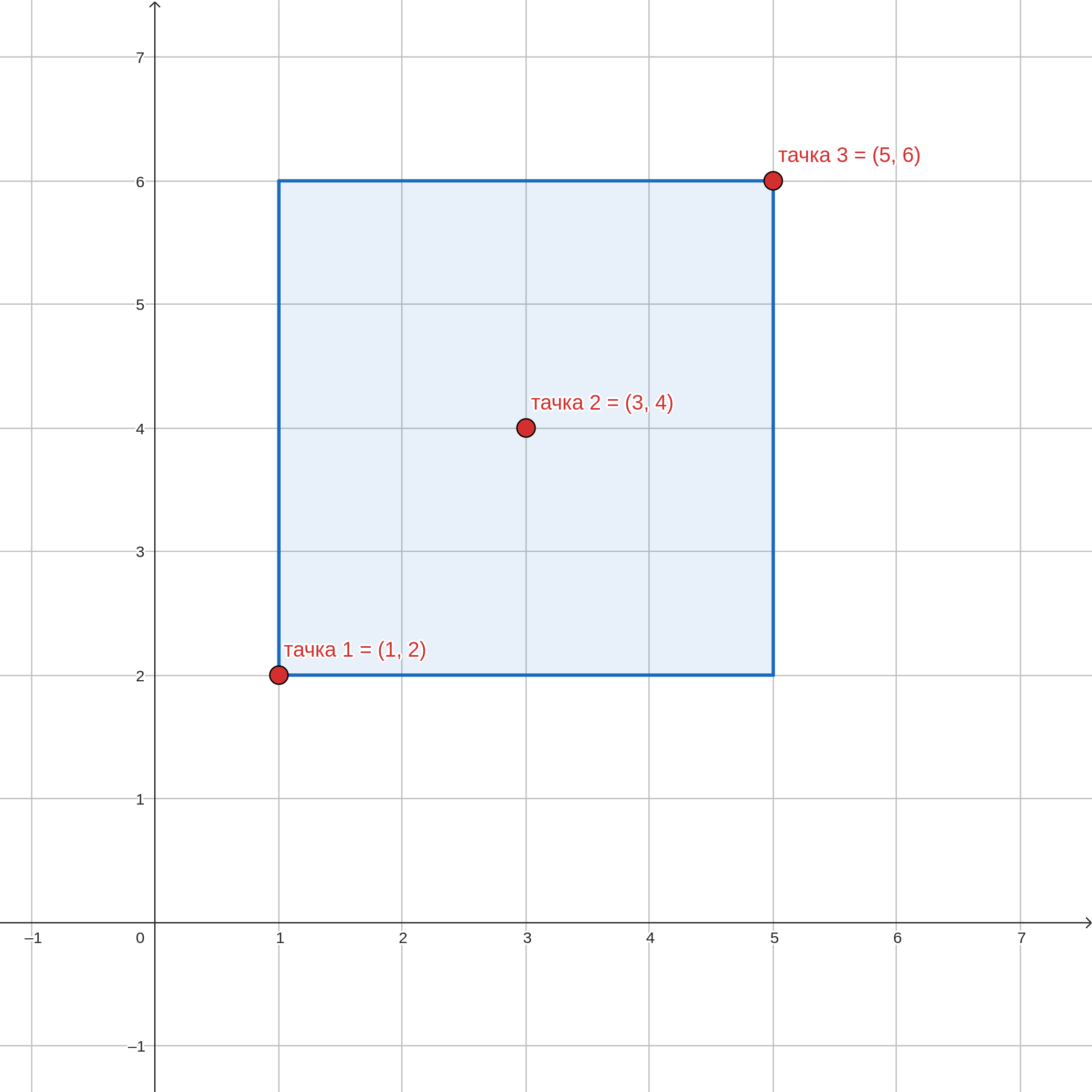
Tri tačke koje su zadate mogu se obuhvatiti kvadratom čije će donje levo teme biti baš u koordinati \((1, 2)\), što je zapravo prvozadata tačka, a gornje desno teme u koordinati \((5, 6)\), što je trećezadata tačka, te je njegova površina \(4^2=16\).

Ograničenja

\(-10^9 \leq x_1, x_2, x_3, y_1, y_2, y_3 \leq 10^9\)

Test primeri su podeljeni u četiri disjunktna skupa:

• U testovima vrednim 30 poena: koordinate su nenegativne \(0 \leq x_1, x_2, x_3, y_1, y_2, y_3 \leq 10^4\)
• U testovima vrednim 30 poena: \(-10^4 \leq x_1, x_2, x_3, y_1, y_2, y_3 \leq 10^4\)
• U testovima vrednim 30 poena: tri tačke su još i kolinearne
• U testovima vrednim 10 poena: Bez dodatnih ograničenja.

Napomena

Smatrati da kvadrat obuhvata, odnosno sadrži tačku čak i ako se ona nalazi na njegovoj stranici ili u temenu.

Autor	Tekst i test primeri	Analiza rеšenja	Testiranje
Vladimir Milovanović	Vladimir Milovanović	Vladimir Milovanović	Aleksandar Višnjić

Glavno rešenje

Za rešenje zadatka dovoljno je pronaći masimum i minimum po svakoj koordinati od tri zadate tačke, a zatim kvadrirati veću od razlika dveju koordinata. Drugim rečima, ako su tri tačke u Dekartovom koordinatnom sistemu zadate koordinatama \((x_1, y_1)\), \((x_2, y_2)\) i \((x_3, y_3)\), tada je najpre neophodno pronaći \(x_\max = \max(x_1, x_2, x_3)\) i \(x_\min = \min(x_1, x_2, x_3)\), te \(y_\max = \max(y_1, y_2, y_3)\) i \(y_\min = \min(y_1, y_2, y_3)\). Da se u zadatku tražila površina minimalnog obuhvatajućeg pravougaonika, onda bi dužine stranica tog pravougaonika bile \(\Delta x = x_\max - x_\min\) i \(\Delta y = y_\max - y_\min\). Međutim, s obzirom da se traži površina minimalnog obuhvatajućeg kvadrata, to je stranica kvadrata zapravo \(\max(\Delta x, \Delta y)\), a površina tog kvadrata \((\max(\Delta x, \Delta y))^2\) do čega se dolazi u konstantnoj vremenskoj i prostornoj složenosti \(\mathcal{O}(1)\). Za sve poene (poslednji podzadatak) bilo je neophodno primetiti implementacijski detalj da kvadriranjem neke velike vrednosti može doći do prekoračenja, pa je u programskom jeziku C rezultat neophodno smestiti u neki dovoljno veliki ceo broj (konkretno long long u ovom slučaju).

Da je umesto tri, u opštijem slučaju bilo zadato \(N\) tačaka u prostoru, mogao bi se primeniti identičan algoritam, a njegova složenost bila bi \(\mathcal{O}(N)\), to jest linearna po broju zadatih tačaka čije se obuhvatanje kvadratom traži.

#include <bits/stdc++.h>

using namespace std;

int main()
{
    vector<int> x(3);
    vector<int> y(3);

    for (int i=0;i<3;i++) cin>>x[i]>>y[i];

    sort(x.begin(),x.end());
    sort(y.begin(),y.end());
    int len=max(x[2]-x[0],y[2]-y[0]);
    cout<<(long long)len*len;
}