4 - Šahovska trka

ZadatakRešenje

Vremensko ograničenje	Memorijsko ograničenje
1000ms	1024MB

Tokom istraživanja starog hrama, Miloš je našao mističnu šahovsku tablu koja ima \(h\) redova i \(w\) kolona na kojoj su neka od polja blokirana uz pomoć magije. On je postao opsednut ovom tablom i krenuo da igra veoma neobičnu igru na njoj.

Na tabli se uvek nalazi tačno jedna figura koju Miloš u toku igre može da zamenjuje drugim figurama. Na početku igre to je kralj koji se nalazi na gornjem levom polju, \((1,1)\). Figure se pomeraju po uobičajenim pravilima šaha, međutim nije moguće staviti ih na blokirana polja. Za svako pomeranje figure Milošu treba 1 sekund. Njegov cilj je da što pre stavi neku figuru na donje desno polje, \((h,w)\).

U proizvoljnom momentu Miloš može da zameni trenutnu figuru nekom drugom figurom na istoj toj poziciji. Međutim, on ne može ovo da uradi trenutno, nego mu za to treba određeno vreme, u zavisnosti od toga koju novu figuru počinje da koristi.

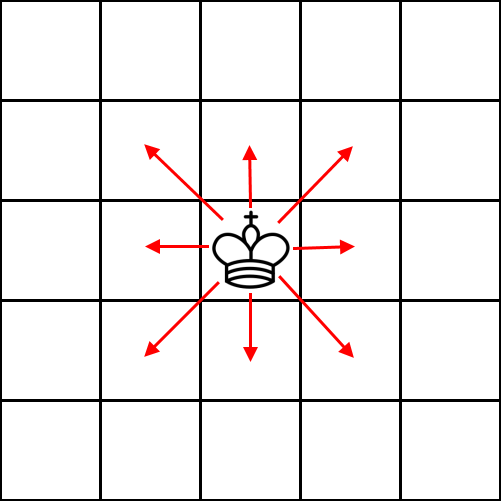Kralj : Milošu treba 1 sekund da zameni bilo koju figuru kraljem.
Kralj se u jednom potezu može pomeriti na jedno od 8 susednih polja ako to polje nije blokirano.

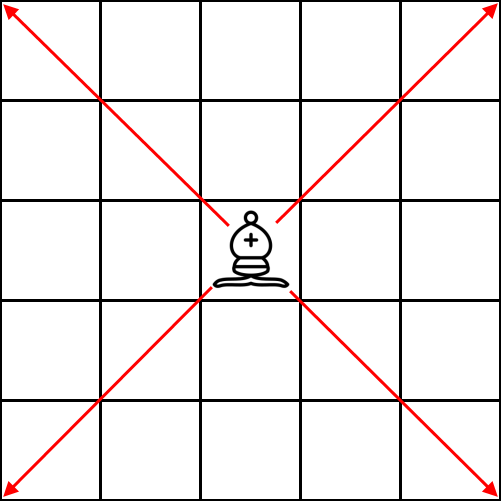Lovac: Milošu treba 2 sekunde da zameni bilo koju figuru lovcem.
Lovac se u jednom potezu može pomeriti dijagonalno proizvoljan broj polja, sve dok ni jedno od polja na njegovom putu nije blokirano.

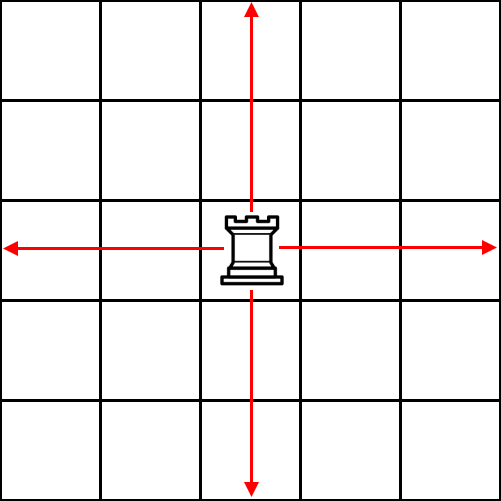Top: Milošu treba 3 sekunde da zameni bilo koju figuru topom.
Top se u jednom potezu može pomeriti levo, desno, gore ili dole proizvoljan broj polja, sve dok ni jedno od polja na njegovom putu nije blokirano.

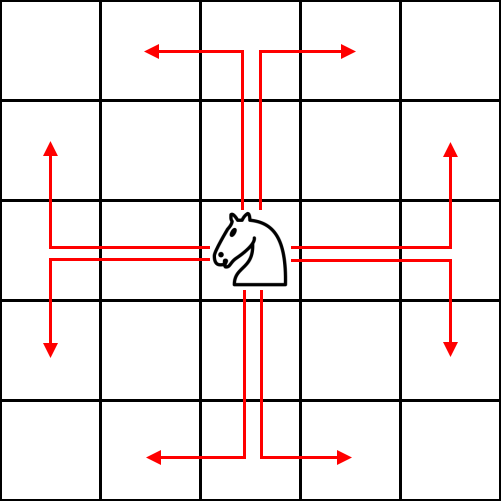Konj: Milošu treba 4 sekunde da zameni bilo koju figuru konjem.
Konj se u jednom potezu može pomeriti 2 polja u proizvoljnom od četiri smera (gore, dole, levo, desno) i 1 polje u jednom od dva smera ortogonalna na prethodni smer. Nije bitno da li su polja preko kojih konj usput prelazi blokirana ili ne.

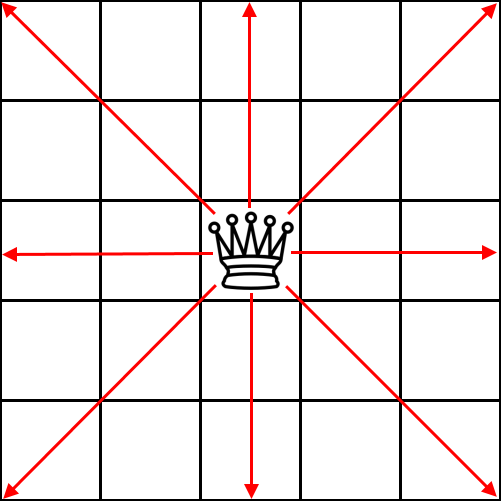Kraljica: Milošu treba 5 sekundi da zameni bilo koju figuru kraljicom.
Kraljica, u jednom potezu, može da se pomeri levo, desno, gore, dole ili dijagonalno proizvoljan broj polja, sve dok ni jedno od polja na njenom putu nije blokirano.

Pomozite Milošu i recite mu za koliko najmanje sekundi može da završi ovu igru, ili mu saopštite da to nije moguće.

Opis ulaza

U prvoj liniji standardnog ulaza nalaze se dva prirodna broja \(h\) i \(w\), koji obeležavaju redom visinu i širinu table. U narednih \(h\) redova se nalazi niz dužine \(w\) koji se sastoji samo od karaktera . i #, gde . označava da je polje slobodno, a # da je polje blokirano.

Opis izlaza

Na izlaz ispisati ceo broj \(t\), najmanji broj sekundi da Miloš postavi figuru na polje \((h,w)\), odnosno \(-1\) ako to nije moguće.

Primer 1

Ulaz

3 3
...
.#.
...

Izlaz

Primer 2

Ulaz

3 5
.####
##.##
####.

Izlaz

Primer 3

Ulaz

10 10
...#.###..
.....#####
...##..#.#
#....#....
.#.......#
##..#.....
......#...
..##..#.#.
..#..#..#.
..#..##...

Izlaz

Objašnjenje primera

Primer 1:

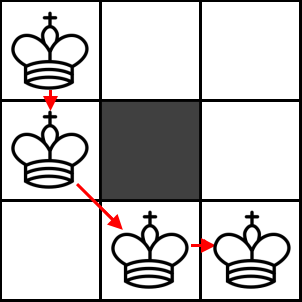
Primer 2:

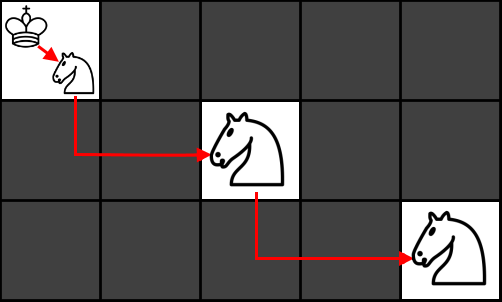
Primer 3:

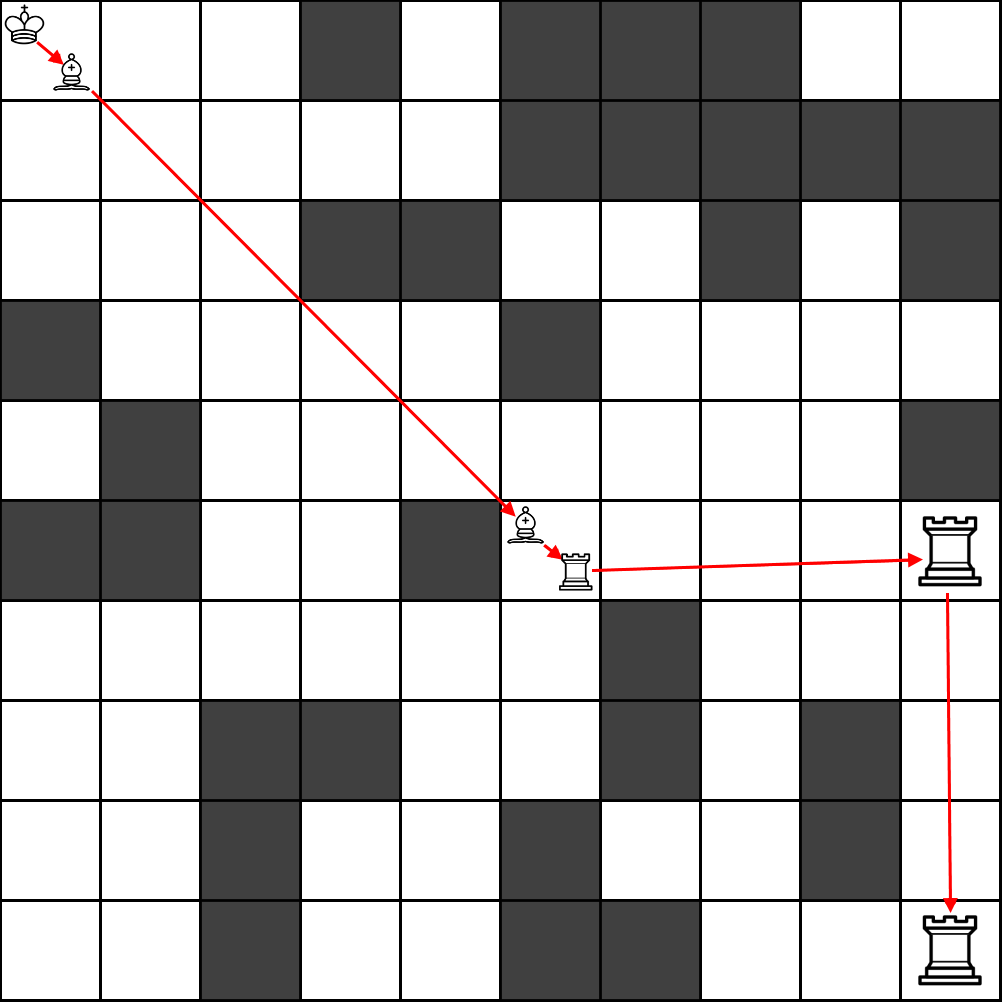
Ograničenja

\(1 \leq h,w \leq 500\)

Test primeri su podeljeni u 5 disjunktnih grupa:

U test primerima vrednim \(10\) poena: \(h,w \leq 5\).
U test primerima vrednim \(10\) poena: \(h,w \leq 200\) i ako postoji rešenje, postoji i optimalno rešenje koje ne zahteva zamenu figura.
U test primerima vrednim \(40\) poena: \(h,w \leq 200\).
U test primerima vrednim \(10\) poena: Ako postoji rešenje, postoji i optimalno rešenje koje ne zahteva zamenu figura.
U test primerima vrednim \(30\) poena: Bez dodatnih ograničenja.

Autor	Tekst i test primeri	Analiza rеšenja	Testiranje
Nikola Pešić	Nikola Pešić	Nikola Pešić	Aleksandar Zlateski

Glavna ideja je da se napravi graf od \(5*h*w\) čvorova gde svaka pozicija na tabli ima po 5 čvorova (jedan za svaku figuru). Grane u ovom grafu predstavljaju sve poteze koje možemo da napravimo i imaju težinu od 1 do 5. Kako bi izbegli \(MLE\), ove grane ne treba da čuvamo u memoriji nego da prođemo kroz njih iterativno kada posmatramo neki čvor. Jedno od rešenja pušta \(Dijkstrin~algoritam\) na ovom grafu kako bi se našla udaljenost svih čvorova od črvora koji predstavlja kralja na poziciji \((1,1)\). Kako bi ubrzali algoritam, tokom prolaženja kroz sva polja na koja može kraljica/top/lovac da ode u nekom smeru, pored uslova da se prekine pretraga kada se stigne na blokirano polje, treba uvesti uslov da se prekine pretraga ako se stigne na polje koje ima istu ili manju udaljenost od udaljenosti trenutnog polja (ne računajući trenutno polje). Vremenska složenost: \(O(n^3 * log n)\), Memorijska složenost: \(O(n^2)\). Još jedna optimizacija programa koja nije bila potrebna za \(100\) bodova je da se umesto \(Dijkstrinog~algoritma\) pusti \(Dialov~algoritam\). Vremenska složenost: \(O(n^3)\), Memorijska složenost: \(O(n^2)\).

04_sahovska_trka.cpp
#include <bits/stdc++.h>

using namespace std;

const int N=500,M=N*N*5,L=5,oo=INT_MAX/N;
int n,m,tr=N*N*L;
vector<string> mat(N);
vector<int> dx={0,0,1,-1,1,1,-1,-1,2,2,-2,-2,1,1,-1,-1},dy={1,-1,0,0,1,-1,1,-1,1,-1,1,-1,2,-2,2,-2},l={0,4,0,8,0},r={7,7,3,15,7},d={1,N,N,1,N};
/*
    Indeksi 0: Kralj
            1: Lovac
            2: Top
            3: Konj
            4: Kraljica
    dx,dy: indeksi 0-3: Smerovi za top
           indeksi 4-7: Smerovi za lovca
           indeksi 8-15: Smerovi za konja
           (Ovo je obelezeno u nizovima l i r)
    d: koliko polja figura sme da se pomeru u tom pravcu
*/
bool inside(int x,int y){
    return x>=0 && x<n && y>=0 && y<m && mat[x][y]=='.';
}
int getNum(int x,int y,int z){ //Iz koordinata polja u broj
    return z + y*L + x*N*L;
}
tuple<int,int,int> getField(int i){ //Iz broja u koordinate polja
    return make_tuple(i/N/L, (i%(N*L))/L, i%L);
}
vector<int> dist(M,oo);
queue<int> q[6]; //Dial's algorithm
int main()
{
    scanf("%i %i",&n,&m);
    for(int i=0;i<n;i++)
        cin >> mat[i];
    q[0].push(0);
    dist[0]=0;
    for(int t=0;t<M;t++)
        while(q[t%6].size())
        {
            int tr=q[t%6].front(),x,y,z;
            q[t%6].pop();
            tie(x,y,z)=getField(tr);
            if(x==n-1&&y==m-1)
            {
                printf("%i\n",dist[tr]);
                return 0;
            }
            for(int i=0;i<5;i++) //Menjanje figure
            {
                int br=getNum(x,y,i);
                if(dist[br]>dist[tr]+i+1)
                    dist[br]=dist[tr]+i+1,q[dist[br]%6].push(br);
            }
            for(int k=l[z];k<=r[z];k++) //Pomeranje figure
                for(int i=1;i<=d[z];i++)
                {
                    int xx=x+dx[k]*i,yy=y+dy[k]*i,br=getNum(xx,yy,z);
                    if(!inside(xx,yy))
                        break;
                    if(dist[br]<=dist[tr]) //Veoma bitan uslov za optimizaciju programa
                        break;
                    if(dist[br]>dist[tr]+1)
                        dist[br]=dist[tr]+1,q[dist[br]%6].push(br);
                }
        }
    printf("-1\n");
    return 0;
}